First, here is the source code. And here is an old win32 build. I don't have a win32 machine so I can't currently produce a new one but I've not made any functional changes to the code. I recently (Mar 2011) spent a couple hours cleaning up and packaging the source code so it will build with no warnings or errors on my current systems. Without a pressing need I'm not going to go in and properly clean up the rest of the code though.
At the time of it's writing (over 10 years ago), it was the fastest general purpose slide puzzle (or sliding block puzzle) solver I knew of. A few others have managed some significant feats but this is still a good solver. The code is a bit crufty and needs a bit of cleanup. Strike that. There's some stuff in there that really makes me cringe. It was written when windows compilers had weird placement (and syntax) of unix system calls. It was also written when I was willing to do such attrocious things as include c files in other c files to avoid creating additional header files.
With regards to some of the design decisions, this was written when I had lots of ram for a home system at 64mb. I'd probably design things differently now that just about any new system has at least 4gb. Something that amuses me now is that I used a simple binary tree and changed the order that I added data to it (so it would stay relatively balanced) rather than just using something like a red black tree. I do think the methods I used should perform marginally better but not enough better that it would have been worth the effort and code mangling.
The following is the writeup that I created many years ago:
This page starts non-technical gets more technical as it goes on. Read as far as you like.
JimSlide is a command line based slide puzzle solver (or sliding block puzzle solver is a more proper and more used term). When I distributed it initially I named it after myself (Jim Leonard) for lack of any better name and just never changed it. While it's interface (a single puzzle definition file to be created in a text editor) takes a bit to get familiar with especially for people who aren't used to working with command line utilities, once the basic syntax is understood it is very easy to set up simple puzzles and has the ability to handle significantly more complex puzzles. It is also the fastest general purpose slide puzzle solver I've found.
To learn how to use the solver read the file readme.txt enclosed in the zip file with the solver or click here to see it online.
I wrote the first incarnations of jimslide a few years ago when slide puzzles were the topic du jour on a puzzle mailing list I subscribe to. There was a fair amount discussion and challenges where puzzles were put forth and better solvers and hardware were brought out to take up the challenge. The solver has evolved a fair amount since then though I've not put any real work on it recently. The solver is several orders of magnitude faster than what was available when I started the project but since the complexity of the puzzle grows exponentially the real difference between what was possible when I started and what is possible now (with JimSlide anyway) is not as great as I'd like to believe it is. Further, for huge puzzles, the duplicate position checking in my solver degrades to a depressing O(n2) whereas in simpler puzzles it's no worse than O(n log n). I've put a fair amount of work into pushing back the transition from O(n log n) to O(n2) to the point where I typically run out of disk space before it gets to that point. Other's who are endowed with better hardware than I might want a better algorithm.
The rest of this page is a general description of the methodologies I use with slight emphasis on things that I felt were innovative.
The basic methodology of my slide puzzle solver is as follows:
One of the first things I realized was that potentially the most expensive and most optimizable part of this procedure is the duplicate position checking. Virtually all of my optimization went towards this aspect of the program.
My first goal was to be able to represent the individual positions in as small a footprint as possible. The reasons are twofold, 1) you can keep more positions in memory at once and 2) comparing two positions for equivalence is faster as long as duplicate (or equivalent) positions are always represented in the same way (thus this became a requirement of the representation). The manner that I chose to represent a position is not extremely complicated but best described by an example
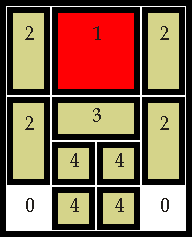
In the slide puzzle pictured above the object is to move the large red square (numbered 1) to where the four smaller squares (labeled 4) are. Each piece is numbered so that equivalent pieces are numbered with the same value and that empty spaces are numbered with a 0. To represent the puzzle in a simple bitstream I walk the puzzle in an ordered fashion and record the value of each piece as I go over it unless I've previously recorded this piece in an earlier position. For example walking each row of the puzzle I would encounter 2112/2112/2332/2442/0440 (the slashes are just to delineate the rows). However since we discard duplicate values for the same piece it goes something like this:
The next problem was how to handle the duplicate checking. The first implementation just used a very memory efficient binary tree. Then I found out that when checking for duplicates, assuming a full width first search, one only needs to check the generation being created, the parent of the generation being created and it's parent (three total generations). I can work this out to myself but am unable to prove it to someone. So I made a new version that has a binary tree for each generation. The fact that I only need to keep three generations in memory is quite a boon. However eventually you do start running out of RAM. Then you start swapping. Quickly you get to the condition where you are incurring one or more page faults per position being checked. Where a location in memory can be fetched in a matter of nanoseconds, a disk read takes several milliseconds. However the disk read penalty is incurred per read rather than per byte read. With large contiguous disk reads (ie greater than a 1Mb or so) the penalty drops considerably to only about a single order of magnitude difference between reading from RAM and reading from disk. With this in mind I went about coming up with more efficient procedure to process the puzzles and this is what I came up with.
First of all create three pools of memory one larger and two smaller pools (call the sizes smallmem and largemem and the pools themselves smallpool1, smallpool2 and largepool). The pools will get used for multiple things in different parts of the process. This is generally considered bad programming style but I'm writing for memory efficiency, not style. Initialize things so the initial position is stored on disk as the previous generation. Each generation is stored on disk in smallmem sized chunks, each chunk just being a flat sorted list of compressed positions. Now that things are initialized we do the following:
This procedure allows me to generate and remove duplicates from lists that are several times the size of main memory with minimal penalty.
I have several other otimizations not listed here, but what is listed here is what I feel makes my program unique.
To find the actual path to the solution, I start at the solution. Record this position and call it the parent position. Generate a list of all of the potential child positions from the parent position and find any of those child positions in the previous generation. Record this position, call it the parent position and list all of the child positions of him. Keep doing this until you find the starting position. You'll find that almost all of this can be done with the routines that were already created to get to the solution.
A couple other optimizations used: